Crabs
Permabanned
- Joined
- Dec 26, 2014
- Messages
- 1,518
I was at Barnes & Noble today and decided to try this Self-Scoring IQ Test designed by the Honorary International President of MENSA, Victor Serebriakoff. There are two tests comprised of verbal, mathematical and spacial questions. I didn't even bother to take the second test because the first one was so frustrating. It made me question how valid IQ testing really is. I thought I would solicit some feedback from the forum regarding a few of these conundrums.
Mistake #1 In the Example below, the third missile is clearly incorrect. (3+2) x 2 = 10, not 12.

Mistake #2 Here is a description of how this problem works:

The piles of blocks shown are solid. Any block without support is shown as such. Each diagram represents a pile of identical blocks. Write a number beside each letter in the column to show how many other blocks touch the block indicated by each letter. A whole face must touch.
We're looking at SA 33 here.
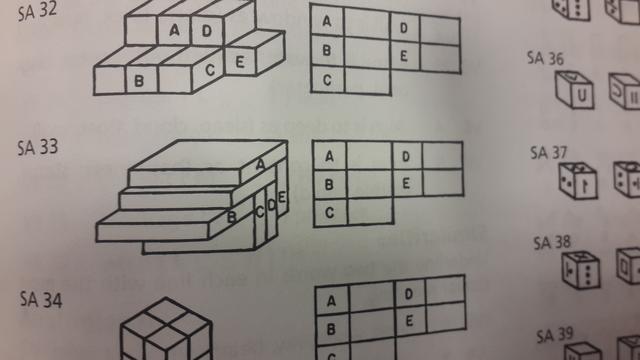
For A, I count one face, which is the edge of E.
For B, I count one face, which is the edge of B.
For C, I count three faces, one broad side of D, the edge of C, and the edge of B.
For D, I count two faces, one broad side of C, and the edge of D.
For E, I count two faces, the edge of E and the edge of one that isn't labeled between A and B.
According to the answers in the back of the book, however... (SA 33) A=2, B=2, C=3, D=3, E=3.

Am I misunderstanding something here? The directions clearly state that a whole face must touch.
Mistake #3 SA 35
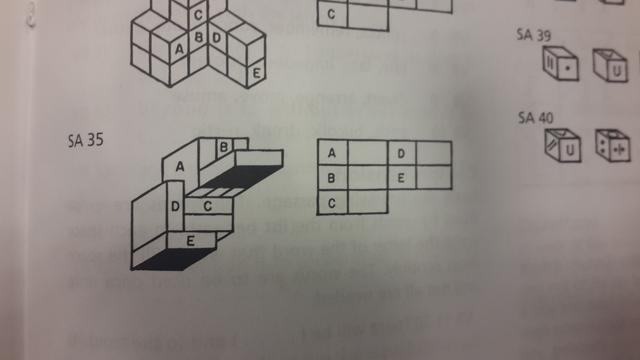
For A, I count one face, the broad side of B.
For B, I count two faces, one broad side of A, and one broad side of an unidentified block.
For C, I count two faces, the edge of C against D and one broad side of an unidentified block below it.
For D, I count three faces, the edge of D against E, the edge of C, and the edge of an unidentified block.
For E, I count one face, the edge of D.
But according to the answers, A=4, B=4, C=5, D=4, E=2. Refer to the answer for SA 35 in the second image above.
Mistake #4
Here is a description of the problem.

In SA 37, each of the three cubes have three images on them, Cubes 1 and 2 share a common image, the two dots. The directions state that the same design does not appear on more than one cube, however, if the first and second cube are the same, we see a total of five different images. The directions clearly say that each cube has two blank faces so how can you have a six-sided cube with five images and two blank faces?
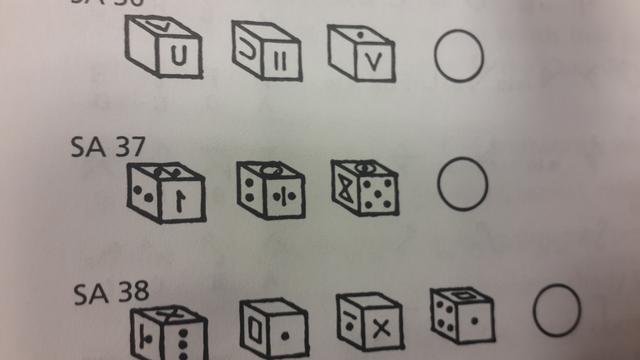
But according to the answers, the first and second cube are the same.
Mistake #5
SA 40 has five different cubes, four of which have three different images, and one of which has two images. There is a total of fourteen different images that we can see. None of the cubes can be the same because the directions state that each cube has two blank faces, therefore there must be five different cubes.
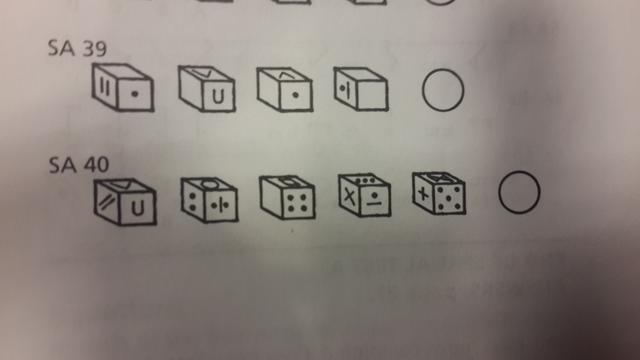
Yet again the answer in the back of the book states that there are three cubes. How can that be?

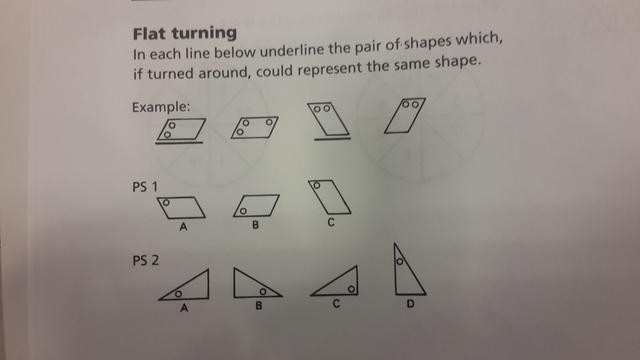
Mistake #6
My issue with these questions is one of semantics. Both questions use the word turn, which suggests a rotation, but in the second image, they apparently mean to flip. The example in the first image is correct, if you turn it clockwise, you get the image that is underlined. In the second image, however, the answer in the example they give is A, which would be correct if you FLIPPED the image upside down. But if you turn it upside down (as in rotate it), it would look more like C, except with the circle in the bottom right-hand corner instead of the bottom left.

Mistake #1 In the Example below, the third missile is clearly incorrect. (3+2) x 2 = 10, not 12.

Mistake #2 Here is a description of how this problem works:

The piles of blocks shown are solid. Any block without support is shown as such. Each diagram represents a pile of identical blocks. Write a number beside each letter in the column to show how many other blocks touch the block indicated by each letter. A whole face must touch.
We're looking at SA 33 here.

For A, I count one face, which is the edge of E.
For B, I count one face, which is the edge of B.
For C, I count three faces, one broad side of D, the edge of C, and the edge of B.
For D, I count two faces, one broad side of C, and the edge of D.
For E, I count two faces, the edge of E and the edge of one that isn't labeled between A and B.
According to the answers in the back of the book, however... (SA 33) A=2, B=2, C=3, D=3, E=3.

Am I misunderstanding something here? The directions clearly state that a whole face must touch.
Mistake #3 SA 35

For A, I count one face, the broad side of B.
For B, I count two faces, one broad side of A, and one broad side of an unidentified block.
For C, I count two faces, the edge of C against D and one broad side of an unidentified block below it.
For D, I count three faces, the edge of D against E, the edge of C, and the edge of an unidentified block.
For E, I count one face, the edge of D.
But according to the answers, A=4, B=4, C=5, D=4, E=2. Refer to the answer for SA 35 in the second image above.
Mistake #4
Here is a description of the problem.

In SA 37, each of the three cubes have three images on them, Cubes 1 and 2 share a common image, the two dots. The directions state that the same design does not appear on more than one cube, however, if the first and second cube are the same, we see a total of five different images. The directions clearly say that each cube has two blank faces so how can you have a six-sided cube with five images and two blank faces?

But according to the answers, the first and second cube are the same.
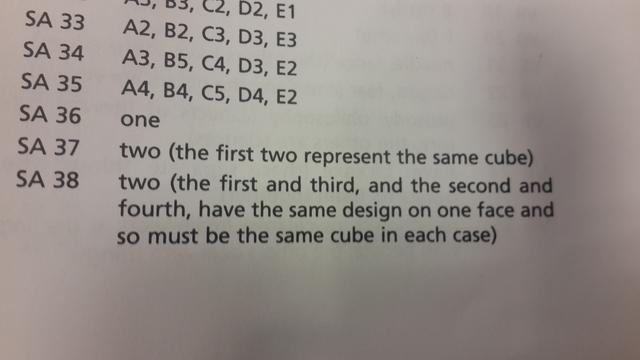
Mistake #5
SA 40 has five different cubes, four of which have three different images, and one of which has two images. There is a total of fourteen different images that we can see. None of the cubes can be the same because the directions state that each cube has two blank faces, therefore there must be five different cubes.

Yet again the answer in the back of the book states that there are three cubes. How can that be?

Mistake #6
My issue with these questions is one of semantics. Both questions use the word turn, which suggests a rotation, but in the second image, they apparently mean to flip. The example in the first image is correct, if you turn it clockwise, you get the image that is underlined. In the second image, however, the answer in the example they give is A, which would be correct if you FLIPPED the image upside down. But if you turn it upside down (as in rotate it), it would look more like C, except with the circle in the bottom right-hand corner instead of the bottom left.


Last edited by a moderator:







