Ok here're some basics ( I am always talking about squares but I mean rectangles of course. Until the last picture where its really squares

):
If you want to find out the area A of an graph like this:
You could do the following:
You take a finite amount of very small quares and add them all up to get the area. "Finite amount of small squares" is called infinitesimal.
You see above that there's still space left between the squares and the graph. To find out the area of the first square you would say: f(a) * h
To not loose the area that is missing between the first square and the graph, you say: f(a+h)*h - f(a)*h = area square one. Or better: [f(a+h)-f(a)]*h
What you get is the median of the upper square and the lower square, but the result would only be a total approximation and be very unprecise. So to get the best results, you'ld have to make the squares very very small.
-----------------
Step 2: Derivation
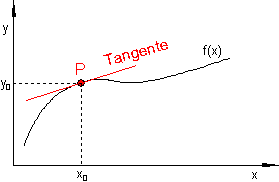
A derivation is the graph of the tangential gradient of another graph in every point.
Here's an example:
You can move the tangent on the whole graph and you always get a new point [x;y]. So a graph that would be for example be : f(x) = x² would produce a graph for its tangential gradient that would be f'(x) = 2x .
This means translated that the graph x² has a gradient of 2x. So if the graph x² would for example show the acceleration of an engine on y-axis and time on x-axis, you can say it will take 2*x seconds to get from i.e. 25 mph to 100 mph.
Now with the derivate showing us every gradiental point in one graph, why not take the points and make lines from them down to x-axis, which serve us as squares for our problem ?
To do that tho we would need the tangential gradient of a graph / function and so we just take our function we already have an say this is a tangential gradient.
This's our initial problem. So lets squeeze the square into a line. This's best done if you let it go as near to zero width as possible. For that the mathematicans use a method called Limen. This is the latin name for the borders of the roman empire. One Limes or fortified wall was built at the Rhine, which they never crossed because the barbarian germans and teutons would have whipped their asses

.
So here's an intresting correlation. While the derivation of a function is it's gradient in every point, the antiderivate of a function or the primitive would be the area the function maps between 2 points and the x - axis (see first picture above).
So as you can see here:
the green area of the red function f(x) between 0 and 2 is obviously 2 squares big. One full + 2 halfes.
And this is how you solve it via integration:
Hope this makes a bit sense. General rule of thumb is: a derivation is a graphs / functions gradient in all points and presents the function f' while a primitive represents the area a graphs maps between two points a,b and the x-axis and is represented by the notation F.