Seymour
Vaguely Precise
- Joined
- Sep 22, 2009
- Messages
- 1,579
- MBTI Type
- INFP
- Enneagram
- 5w4
- Instinctual Variant
- sx/so
Reynierse being brought up in another thread made me think of Wilde once again, and so I reviewed his book again. On rereading, I do think he gives a reasonable way to map the function-attitudes (what he calls "modes") in a post Type Dynamics (TD) world. Note that Wilde starts from Reynierse's model that preferences are continuous (not dichotomous), and that strength of preference correlates to how much one prefers (and acts upon) one's preferences.
So, really his approach of applying to this to the function-attitudes ("modes") is pretty straightforward. When one considers something like the descriptions of Te (extraverted thinking), one can break it down into it arising out of a combination of preferences.
Te as an Example
It's clear that descriptions of Te have Extraverted qualities (about judging and controlling externally), Thinking qualities (based on logical, objective measures of utility) and Judging qualities (it's a form of judgment: is about planning, closure, etc). That's all pretty unsurprising and definitional.
So, if one were going to thinking about the platonic ideal of a ESTJ or ENTJ, for example, one would think of someone who's 100% Extraverted, Thinking and Judging. We'd expect such a person strongly prefer Te and express it habitually.
But let's take a less extreme case... an ESTJ who is only slightly extraverted. We'd expect to see this person somewhat less engaged externally, so Te (while still present) wouldn't be quite so prefered or expressed.
Or, consider an ENTJ who has a weak J preference. We'd expect to see less emphasis on closure, planning, etc.
So, we could extrapolate that strong preference for E+J = strong preference for Je (extraverted judging). And, conversely, strong preference for I+P = strong preference for Ji (introverted judging).
We can farther extrapolate the same thing for perceiving. Strong preference E+P = strong Pe. Strong preference for I+J = strong Pi.
We could graph this relationship like so:

Where the red arrow indicate the Ji <-> Je axis (conceptually extending to the corners of the graph), and the blue arrow indicates the Pe <-> Pi axis (also conceptually extending to the corners of the graph).
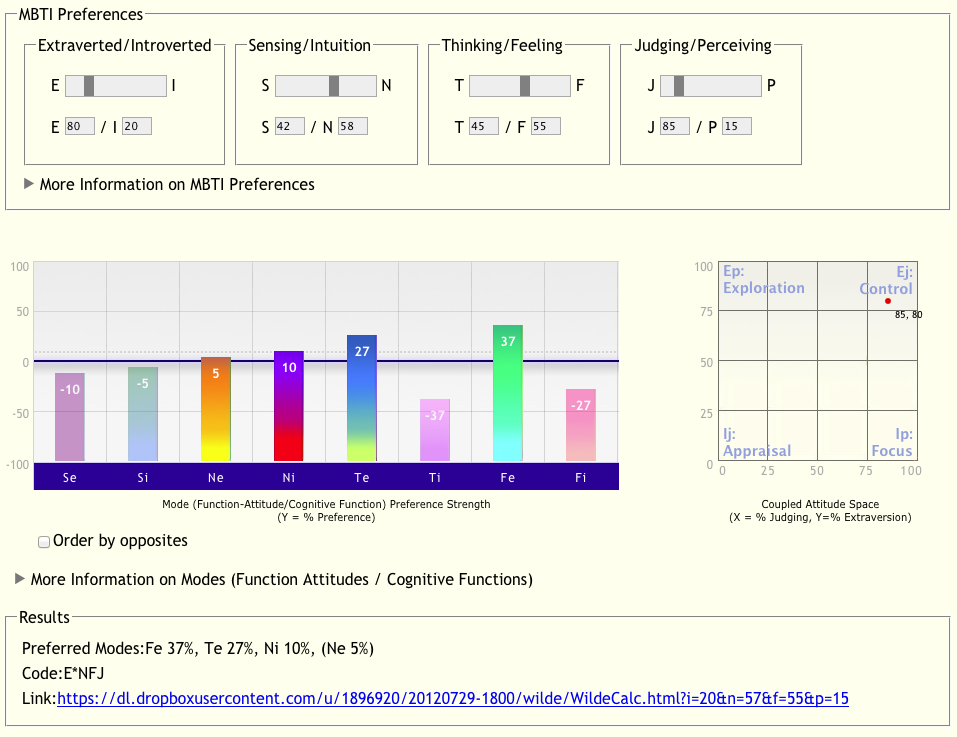
We could map the ideal/pure ESTJ like so (see purple X in upper right):

We could then imagine some additional cases. Suppose someone has strong E+J preferences, and a middling T/F preference. We'd expect such a person to prefer Je, but be more flexible about using Te (that is, be flexible about sometimes seeing things from more of an Fe perspective).
Additional Differences from Traditional Type Dynamics
Another interesting quality of this layout when on falls on the red judging line (in the graph above, where one's E/I preference is approximately equal to one's J/P preference... that is your E~J or I~P, where "~" means aproximately equal). In that case, your Je vs Ji preference is going to be approximately balanced... meaning you your Se/Si or Ne/Ni preference may be almost equal.
The some goes when one's judging preference falls along the blue judging line (also as above, but extending to the corners of the graph). If your perferences are E~P or I~J, then you may have two judging preferences that are similar (Te & Ti, or Fe & Fi).
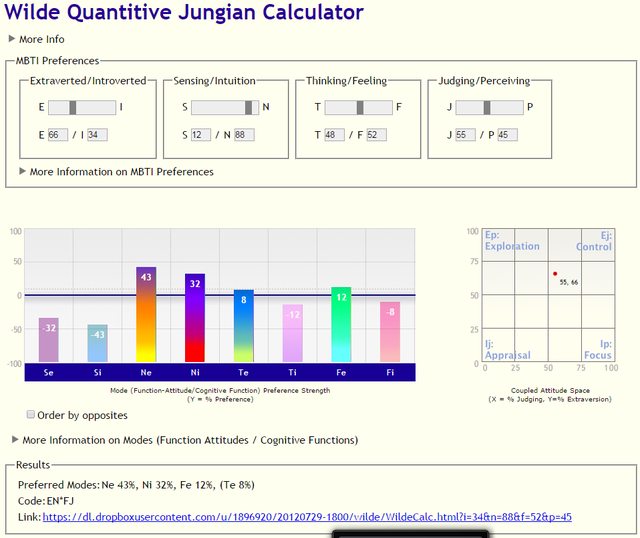
In this approach, there are also cases where one can lead with two modues/functions in the same orientation. For example, if one is strong E, S, T and moderate P, one could lead with Se & Te (followed by Ti and Si):

These cases are not represented in traditional type dynamics, but do seem true to life in some cases (like my parter, who is ISTJ-esque but leads with Si and Ti).
Corner Cases
In additional to the above cases, there are also cases where the mode/function calculations seems a little mismatched to the traditional definitions of the functions.
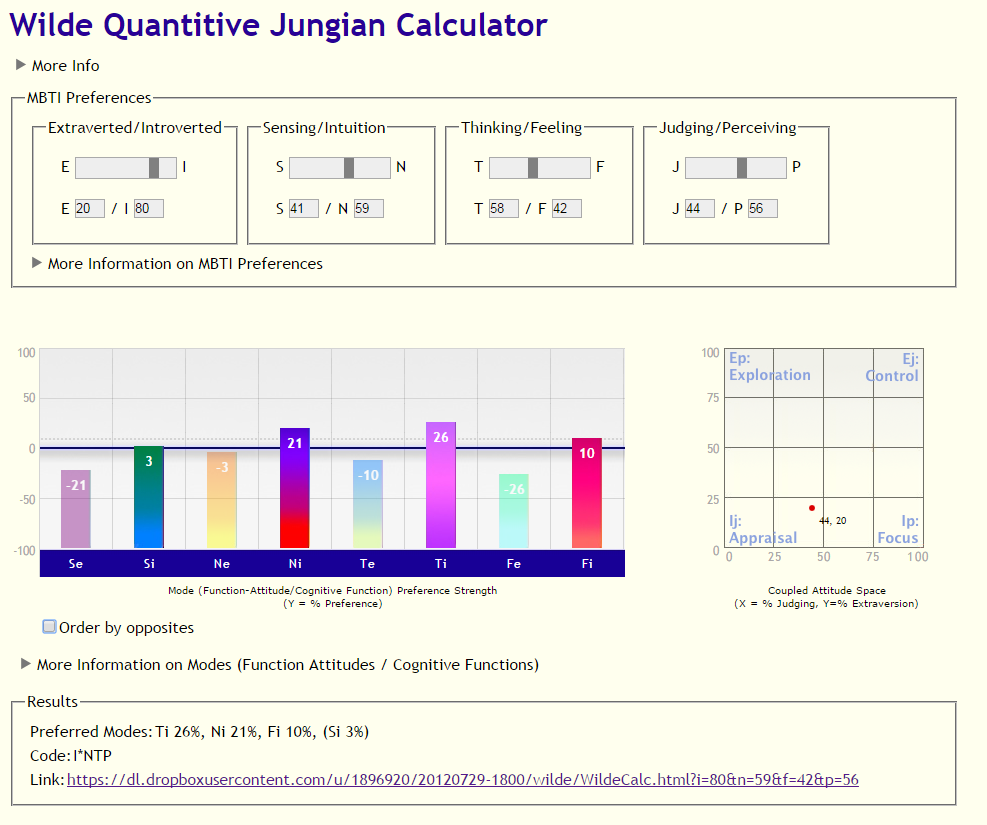
In my case, which is something like this, Wilde's formulas claim I prefer Fi, Ni, Ne and Ti (in that order):

I generally find that to be moderately close to my actual strengths, except for the Ni part. Why doesn't the Ni seem to fit well? Well, it has to do with Ni in Wilde's model being comprised of I, N and J.
In my case, I'm strongly perceiving; so insofar as Ni = N+J, Ni isn't a good fit for me (because of the lack of much judging preference). I'm not good at long term planning; I'm not particularly aware of trends over time; I don't tend to seek closure.
Conversely, insofar as Ni is I+N, Ni is not a terrible fit. I don't rush into external action, I like to mull things over internally before expressing them, and I don't require much internal stimultation to fuel a lot of internal thought (introversion qualities). I also strongly prefer intuition.
So, there are limitations to Wilde's calculations, in that the functions (as they are defined today) or the combination of three different preferences. Depending on specifics, you may end up not falling into one of the preferences that contribute to a function/mode, and so your usage of the function/mode may match the traditional definition that well. In those cases, I think it pays to think of the function/mode as its component parts, and figure out which ones make sense.
Adjustments
If I were going to tune Wilde's formulas to fit better with traditional function definitions, I think I might weight things a bit towards the J/P scale, and a bit less towards the E/I scale, such that an "ideal" or "extreme" ESTJ would favor Si over Se. That would also, presumably, adjust my case to favor Ne over Ni.
Conclusion
Regardless, I think Wilde's approach is a useful one, and one that better matches observed strengths and behaviors than traditional Type Dynamics. While I think it's particularly strong when applied to balancing team composition (Wilde's primary focus), it's still useful in other realms. It also serves as a means of adapting some of the description power of the functions/modes to an empirically-based worldview... one truer to reality than traditional type dynamics.
I also think it makes one wonder about grouping by other preference pairs (or triads), and seeing what insights might arise. I can image large group exercises partitioning people into groups of EJ/EP/IJ/IP, ES/EN/IS/IN, ST/SF/NT/NF (or some other combination of preference pairs/triplets). There's no reason those couldn't be just as illuminating as grouping by function/mode, or grouping by Kiersey's temperaments (SJ/SP/NT/NF).
So, really his approach of applying to this to the function-attitudes ("modes") is pretty straightforward. When one considers something like the descriptions of Te (extraverted thinking), one can break it down into it arising out of a combination of preferences.
Te as an Example
It's clear that descriptions of Te have Extraverted qualities (about judging and controlling externally), Thinking qualities (based on logical, objective measures of utility) and Judging qualities (it's a form of judgment: is about planning, closure, etc). That's all pretty unsurprising and definitional.
So, if one were going to thinking about the platonic ideal of a ESTJ or ENTJ, for example, one would think of someone who's 100% Extraverted, Thinking and Judging. We'd expect such a person strongly prefer Te and express it habitually.
But let's take a less extreme case... an ESTJ who is only slightly extraverted. We'd expect to see this person somewhat less engaged externally, so Te (while still present) wouldn't be quite so prefered or expressed.
Or, consider an ENTJ who has a weak J preference. We'd expect to see less emphasis on closure, planning, etc.
So, we could extrapolate that strong preference for E+J = strong preference for Je (extraverted judging). And, conversely, strong preference for I+P = strong preference for Ji (introverted judging).
We can farther extrapolate the same thing for perceiving. Strong preference E+P = strong Pe. Strong preference for I+J = strong Pi.
We could graph this relationship like so:

Where the red arrow indicate the Ji <-> Je axis (conceptually extending to the corners of the graph), and the blue arrow indicates the Pe <-> Pi axis (also conceptually extending to the corners of the graph).
We could map the ideal/pure ESTJ like so (see purple X in upper right):

We could then imagine some additional cases. Suppose someone has strong E+J preferences, and a middling T/F preference. We'd expect such a person to prefer Je, but be more flexible about using Te (that is, be flexible about sometimes seeing things from more of an Fe perspective).
Additional Differences from Traditional Type Dynamics
Another interesting quality of this layout when on falls on the red judging line (in the graph above, where one's E/I preference is approximately equal to one's J/P preference... that is your E~J or I~P, where "~" means aproximately equal). In that case, your Je vs Ji preference is going to be approximately balanced... meaning you your Se/Si or Ne/Ni preference may be almost equal.
The some goes when one's judging preference falls along the blue judging line (also as above, but extending to the corners of the graph). If your perferences are E~P or I~J, then you may have two judging preferences that are similar (Te & Ti, or Fe & Fi).
In this approach, there are also cases where one can lead with two modues/functions in the same orientation. For example, if one is strong E, S, T and moderate P, one could lead with Se & Te (followed by Ti and Si):

These cases are not represented in traditional type dynamics, but do seem true to life in some cases (like my parter, who is ISTJ-esque but leads with Si and Ti).
Corner Cases
In additional to the above cases, there are also cases where the mode/function calculations seems a little mismatched to the traditional definitions of the functions.
In my case, which is something like this, Wilde's formulas claim I prefer Fi, Ni, Ne and Ti (in that order):

I generally find that to be moderately close to my actual strengths, except for the Ni part. Why doesn't the Ni seem to fit well? Well, it has to do with Ni in Wilde's model being comprised of I, N and J.
In my case, I'm strongly perceiving; so insofar as Ni = N+J, Ni isn't a good fit for me (because of the lack of much judging preference). I'm not good at long term planning; I'm not particularly aware of trends over time; I don't tend to seek closure.
Conversely, insofar as Ni is I+N, Ni is not a terrible fit. I don't rush into external action, I like to mull things over internally before expressing them, and I don't require much internal stimultation to fuel a lot of internal thought (introversion qualities). I also strongly prefer intuition.
So, there are limitations to Wilde's calculations, in that the functions (as they are defined today) or the combination of three different preferences. Depending on specifics, you may end up not falling into one of the preferences that contribute to a function/mode, and so your usage of the function/mode may match the traditional definition that well. In those cases, I think it pays to think of the function/mode as its component parts, and figure out which ones make sense.
Adjustments
If I were going to tune Wilde's formulas to fit better with traditional function definitions, I think I might weight things a bit towards the J/P scale, and a bit less towards the E/I scale, such that an "ideal" or "extreme" ESTJ would favor Si over Se. That would also, presumably, adjust my case to favor Ne over Ni.
Conclusion
Regardless, I think Wilde's approach is a useful one, and one that better matches observed strengths and behaviors than traditional Type Dynamics. While I think it's particularly strong when applied to balancing team composition (Wilde's primary focus), it's still useful in other realms. It also serves as a means of adapting some of the description power of the functions/modes to an empirically-based worldview... one truer to reality than traditional type dynamics.
I also think it makes one wonder about grouping by other preference pairs (or triads), and seeing what insights might arise. I can image large group exercises partitioning people into groups of EJ/EP/IJ/IP, ES/EN/IS/IN, ST/SF/NT/NF (or some other combination of preference pairs/triplets). There's no reason those couldn't be just as illuminating as grouping by function/mode, or grouping by Kiersey's temperaments (SJ/SP/NT/NF).